Survival Guide - Encryption, Authentication
This is a survival guide covering the mind-numbing topics of Cryptography, Encryption, Authorization and Authentication. For the mathematically challenged (and who is not) the maths involved in cryptography are gruesome in the extreme and are covered, if at all, at the level of 'stuff happens'. The guide concentrates on system functionality and consists almost exclusively of descriptions, diagrams and explanations rather than specific commands or implementations. Much of this stuff is background for SSL/TLS and X.509 certificates in which there are enough commands and implementation descriptions to give you a hearty buzz for the rest of your life.
Contents:
Terminology
A non-exhaustive list of terms used in security. Many of these terms are explained further in the text others are left dangling either to create a sense of tension in the reader or, more likely, because we have no idea what they mean.
| Authentication |
The process or procedures used to verify that data or information asserting that it originates from a source can only have come from that source. Techniques used include digital signatures, MACs and even good 'ole passwords. Once Authenticated you will, typically, still need to be Authorized to access specific resources or information. |
| Authorization |
When a user has Authenticated they are typically Authorized, based on their login credentials or account properties, to access, or denied access to, certain systems resources such as files, applications or network resources. The term privilege is sometimes used synonymously for Authorization, thus, a user may have enough privileges to access resource X but not resource Y. They are Authorized to access X but not Authorized to access Y. |
| Asymmetric |
See full definition. |
| Bit Strength |
Is defined in bits and is a measure of the amount of work needed to break a cryptographic algorthm. Bit Strength provides a method to measure the relative strength of one encryption alogithm against another. Depending on the algorithm the Key Size and Bit Strength may, or may not, be the same. NIST Publication SP 800-57 Part 1 Section 5.6.1 defines bit strength in excuriating detail. NIST's current recommendation (2010 to 2030) is that a cipher have a minimum bit strength of 112 bits. There is a simplified bit-strength to key size comparison chart on this page |
| Cipher |
A cipher a.k.a. an encryption algorithm. To cipher a.k.a. the process of encryption. |
| Clear Text |
A.k.a. plain text. A block of data to which no encryption process has been applied or a block of data that results from a decryption or deciphering operation. |
| Credentials |
A fancy name for what most of us would call a password (though it can take other forms such as a hardware token or biometric details). Your credentials are a way of proving that you are who you say you are. Since you should be the only person (or group of persons in some cases) who know or have access to your credentials, when you present them to a system or network it proves that you are who you say you are. After some form of exchange which will include presenting your credentials (for instance, typing in a password) you will be Authenticated. Once Authenticated you, typically, will still need to be Authorized to access specific resources or information though many systems imply the authorization from the authentication. Thus, say, authenticating as root in a 'nix system will grant authorization to all resources whereas authenticationg as a normal user will only grant authorizations based on the user and group name. |
| Decipher |
Apply a decryption algorithm to an encrypted block of text and, given the appropriate key(s), turn it into plain text. Most, but not all, ciphers use the same algorithm to encrypt and decrypt. |
| Digest |
See Hash |
| Encryption |
The process of transforming data using a cipher (a.k.a. an encryption algorithm). Techniques used may be symmetric or asymmetric. |
| Fingerprint |
See Hash |
| Forward Secret |
a.k.a. Forward secrecy. This refers to the characteristic whereby if a long duration secret, for example, the private key of an asymmetric algorithm is compromised an attacker cannot decrypt previous conversations or sessions. This is typically done, as in the case of TLS/SSL, by computing session keys with a randomized seed. |
| Hash |
A.k.a. digest, message digest, one-way hash or fingerprint. An algorithm for reducing an infinitely large block to a unique octect string of a fixed and significantly smaller size - for example 128 or 256 bits (16 or 32 octets). The term one-way hash is occasionally used since is clearly indicates that the original message message cannot be recreated from the hashed form. Hashes ensure message integrity and are used in MACs and digital signatures. The term fingerprint is occasionally used in the sense that a fingerprint is a substitute for the whole person, so the hash becomes a fingerprint that may be stored or transmitted independently of a message or data but can always to used to verify the integrity of the data in any given message. |
| Key Size |
A.k.a. key length. The number of bits used for the key of an encryption algorithm; in general, the more bits the stronger the cipher. Many algorithms can take variable key sizes allowing them to be progressively strengthened over time. Key length (key size) should not be confused with the Bit-Strength of a cryptographic implementation. Thus, an RSA Key length/Key size of 2048 bits has a Bit-Strength of 112 bits. |
| Message Digest |
See Hash |
| Non-Repudation |
If an entity - person or system - is authenticated then, as described above, they/it is proven to be who they say they/it are. They/it cannot subsequently deny (repudiate) the authentication. Thus, if an entity authenticates succesfully to, say, a financial system and withdraws 10 zillion moolah they cannot subsequently deny (repudiate) the transaction. |
| One-way Hash |
See Hash |
| Password |
See Credentials |
| Plain Text |
A.k.a. clear text. A block of data to which no encryption has been applied or a block of data that results from a decryption or deciphering operation. |
| Shared Secret |
Refers to the single key of a Symmetric encryption alogorithm in which all parties to the secret conversation must have a copy of (share) the same key. |
| Symmetric |
See full definition. |

Cryptographic Overview
Cryptography according to Webster is "the enciphering and deciphering of messages in secret code or cipher; also : the computerized encoding and decoding of information".
It is the process of transforming (enciphering or encrypting) data (called clear or plain text) using some process (a cipher or encryption algorithm) into some gobbledygook that can only be transformed back (deciphered or decrypted) into plain text if the recipient has some some secret knowledge such as a key or a set of keys.
Historically the ciphers, or encryption algorithms, used formed the secret. For example - shift every character one position left (the cipher) - that we used as kids when sending secret messages to our friends. The weakness here is that if the method or encryption algorithm (the cipher) is discovered all communication sent using that algorithm (or cipher) can be converted into plain text (deciphered). A new algorithm has to be created and propagated to all parties before we can start sending messages again.
Modern cryptography assumes that the bad guys will discover the cryptographic algorithm, indeed, for reasons we will see later, the algorithms themselves are widely published. Instead, the secret lies with a unique key or keys which are used by the algorithm to transform (encipher or decipher) the data. If the key is exposed or compromised (a.k.a stolen by a bad guy) then by simply replacing the key, but keeping the algorithm the same, confidential communication can recommence. The bad guy has to start all over again to discover the key with no greater knowledge than before but with, hopefully, tightened end-user key security procedures in place.
Cryptographic algorithms are not provably (in a mathematical sense) secure. Instead, they are widely published and exposed to repeated attack by dedicated researchers and specialists (black hat testers) who love this kind of stuff. Only having resisted repeated and sustained attacks are the algorithms used operationally. Since research into the cryptographic algorithms is ongoing it can occasionally mean that apparently robust, mature algorithms need to be replaced when weaknesses are discovered. A recent example here relates to theoretical weaknesses being discovered in the MD5 digest algorithm around 2004.
While it is always possible to use a brute force attack to find a key, cryptographic systems use a concept known as computationally infeasible (a termed coined by Diffie and Hellman in their seminal paper) which simply means that it would cost too much or take too long to mount such a brute force attack. Computationally infeasible is based on today's technology and is therefore a relative not absolute definition and does change over time. Thus, for example, in some algorithms the key size is typically increased over time as raw computational capacity increases.
If a secret key, or keys, are obtained by an attacker (by stealth, brute force, luck or other nefarious means) then the last thing they are likely to do is to boast about it, which will only trigger the user to replace the key(s). Instead, the bad guys will simply and quietly continue to eavesdrop on supposedly secure communications. This is a serious problem and is typically handled by some combination of maintaining the keys in a 'tamper-proof' (which will destroy the key if a compromise is attempted) or a 'tamper-aware' environment (a.k.a. an HSM, which will alert the user if the key is compromised) or by regularly changing the key, called key maintenance, which simply minimises any potential damage. There is no way to know or prove that a key has been compromised other by observing, typically negative, consequential effects.
Operational Note: Many cryptographic algorithms have been around and remained unmodified for many years (> decade in some cases). Many standards were written suggesting a range of cryptographic algorithms but mandating, typically, only one to ensure some form of common demoninator. However, as computational speed increases and cryptographic attacks become increasingly frequent (in some cases from sources that were supposedly benign) the need to change, either algorithm or key size, is becoming of growing importance. This process - known as algorithmic agility in the endless jargon - can pose a serious operational problem for legacy systems.
Cryptography may be used for three purposes:
Confidentiality: Only the parties to the communication can understand the messages or data sent between the parties.
Authentication: The data could only have come from a known source.
Integrity: The data received by one party was the data sent by the other party and was not manipulated or compromised during transmission.
One or more of the above may be provided by a single algorithm or may be provided by a combination of algorithms and methods.
First the basic techniques. Modern cryptographic techniques are either symmetric or asymmetric.
Note: One of the better sources of cryptographic information is contained in the US government National Institute of Standards and Technology (NIST) set of publications. In particular SP800-57 Part 1 (currently rev 4 2016) discusses key management and provides an excellent and thorough analysis of both cryptographic methods and threats. It further provides practical advice on key sizes for various algorithms in Tables 2 and 4. Any interested reader is well advised to plough through this worthy, if long, document for a highly practical and thorough grounding in the arcane subject of cryptography. A number of other NIST SP documents are referenced throughout this page.
Finally, the insatiably curious reader could do no better than read the paper that started the public key revolution, New Directions in Cryptography (1976) by Whitfield Diffie and Martin Hellman. A bit heavy on the math in places but these can be mercifully skipped without losing the cystal clarity of the ideas. Clear, readable prose, most unusual for this type of paper. A worthy investment in time.

Symmetric Cryptography
Symmetric encryption algorithms, also called single-key, shared-secret, or even, confusingly, private-key systems, use a single key (or set of keys) to encrypt and decrypt the data. This single key - the shared secret - must be securely exchanged between the parties that will use it prior to the actual secure communication. The limitations of shared-secret systems are twofold. First, the key must be distributed securely using a process called key management, which itself is not trivial. Second, the method of securing the key once distributed lies with all the parties to the communication: "I trust myself but do I trust all the other parties to keep the key secret?". If a shared-secret key is compromised at any of the parties then it is compromised for all parties that use it. Symmetric algorithms use significantly less computational resources than their asymmetric counterparts. They are, generally, the only viable method for encrypting bulk data streams.
Examples of common symmetric key algorithms are DES (Data Encryption Standard a.k.a Data Encryption Algorithm (DEA), Triple DES (TDES a.k.a. TDEA (Triple Data Encryption Algorithm)), AES (Advanced Encryption Standard), IDEA (International Data encryption Algorithm), and RC4 (Rivest Cipher 4 - as of 2013 regarded as capable of being cracked, though attacks not yet proven or published), and typical key sizes are 64, 128, 192 or 256 bits. Figure 1 shows the operational use of a shared secret for classic confidential communications. Note: The term shared secret, which describes a single key (or set of keys) used, or shared, by both ends of the communication should not be confused with secret sharing, which describes a process whereby the shared, or single, secret key is broken up into parts and shared between multiple persons to make it more secure.
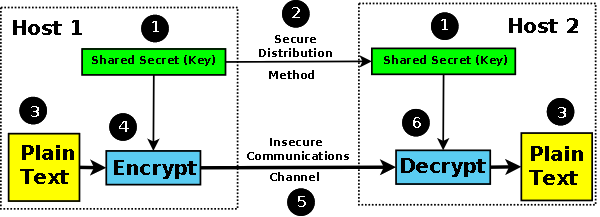
Figure 1 - Symmetric Cryptography

Asymmetric Cryptography
Asymmetric encryption algorithms use a pair of keys - a public and a private key - and are generally referred to as public-key cryptographic systems or sometimes as nonsecret encryption (somewhat of an oxymoron). In these systems, data (called plain-text in the jargon) that is encrypted with one key can only be decrypted with the paired key. Given one key, it is computationally infeasible to derive the paired key. Asymmetric encryption works by making one key, called the public key, widely available, while maintaining the other key, surprisingly called the private key, a secret. This process has an interesting side effect. If a message is encrypted with a private key and can be decrypted with its paired public key, then only the owner of the private key could have done it. This property is used in digital signatures and is described later. Asymmetric algorithms use significant computational resources in comparison with their symmetric counterparts and therefore are generally not used to encrypt bulk data streams.
The most widely used public-key encryption systems are RSA (after the inventors Rivest, Shamir, and Adelman), DSA (Digital Signature Algorithm) and Elliptic Curve Cryptography (ECC or just EC). Typical key sizes for RSA public-key systems are 1024 and 2048 bits (the current US NIST recommendation to cover the period from 2010 until 2030), or even higher if you enjoy causing excessive use of CPU resources in decryptors. Elliptic Curve Cryptography (ECC) uses typically smaller bit sizes, examples, 160, 233, 283, 384 or 571. The public keys of a private/public key pair can be safely stored in a public service, such as DNS, while the private key must be maintained securely in a private location (or increasingly in Hardware Security Modules (HSMs)). Figure 2 illustrates the use of public-key cryptography for classic confidential communications.
Note: While the current NIST recommendation until 2030 is for a 2048 RSA key, RFC 8603 mandates use of RSA with 3072 or 4096 ((or ECDSA P-384) for X.509 certificates used in CNSA (Commercial National Security Algorithm) Suite.
Bit-strength to key size table.
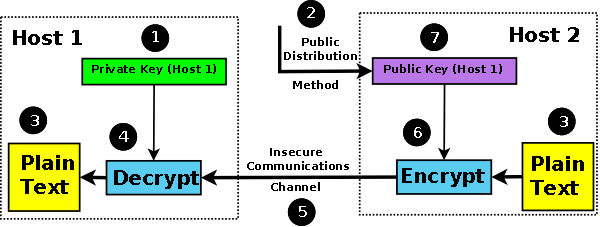
Figure 2 - Asymmetric Cryptography
To achieve confidentiality, a message to be sent from Host2 to Host1 is encrypted with the public key of Host1. Only the private key of Host1 can decrpyt this message. If Host1 wishes to send a confidential message to Host 2 then it must obtain the public key of Host2 (not shown in diagram 2 to avoid unnecessary complexity).
Public-key systems have one significant limitation. They rely on knowing, or trusting, that the public key which will be used in communications with a person, organization or entity really is the public key of the person or organization and has not been spoofed by a malicious third party. There are two broad methods by which this is usually accomplished. A Public Key Infrastructure (PKI), or more commonly by the use of a trusted third party. The third party securely manages, and attests to the authenticity of, public keys. If the third party (a.k.a. a Certificate Authority (CA) in the context of X.509 certificates) is requested to provide the public key of X, they are trusted to provide the correct public key. The third party is trusted to have satisfied themselves by some process - attestation, notarization, or another process - that X is the one and only, or globally unique, X. The most common method for making available public keys that have been verified by a third party is to embed them in an X.509 (or SSL) certificate which has been digitally signed by the the issuer (typically a Certificate Authority (CA)).
Notes on RSA versus Elliptic Curve Performance:
RSA has been around since approximately 1977 and Elliptic Curves Cryptography (ECC) since 1985. Due to the widespread adoption of RSA (in 2018 it was the dominant public key encryption method) it has been widely studied for exploits and optimized implementations exist for most machine architectures. ECC is much less studied and therefore may, or may not, still yield some surprises. ECC implementations have probably not yet reached peak efficiency and therefore the comparisons below should be treated with some caution but will likely remain generally true.
While it is almost a no brainer that mobile devices will prefer ECC due to lower CPU loads and smaller bandwidth requirement when receiver, say, web pages (decrypt function), web servers will see significant increases due to the increased performance requirement of ECC encryption and would probably love to keep on using RSA.
Bit-Strength Comparison
Table extracted from NIST Publication SP 800-57 Part 1 Section 5.6.1 Table 2.
| Bit-Strength |
RSA |
ECC |
| 80 |
1024 |
160-233 |
| 112 |
2048 |
224-255 |
| 128 |
3072 |
256-383 |
| 7680 |
7680 |
384-511 |
Asymmetric Algorithms and Quantum Computers
Both RSA and ECC asymmetric algorithms use complex integer mathematics (typically prime numbers) and consequentially will become highly insecure in a quantum computing world. A new generation of algorithms that will work in a quantum world is slowly emerging. RFC 8554 describes an algorithm known as LMS (Leighton-Micali Signature) and using a One-Time Signature (OTS) that will, it is hoped, survive the quantum world. These algorithms require system designers and implementors to carefully consider the implications of using this new generation of algorithms, which, coupled with the lack of operational experience means the RFCs are published for experimental purposes and have Informational status. However, their significance should not be underrated.

(Ephemeral) Diffie-Hellman Exchange
The Diffie-Hellman exchange (DH) is a method by which two (or in some case more) peers can independently create the same shared secret that may be subsequently used in a symmetric cryptographic algorithm (TLS, for example uses DH to create the key used for the Data Record phase). It is assumed that the entire session during which the two peers communicate can be evesdropped by a third party. The third party cannot derive the same key because it lacks certain information.
The original Diffie-Hellman Exchange (now frequently referred to as Finite Field Diffie-Hellman) uses exotic maths:
Y (shared secret) = g (a generator) ^ X (a secret key) mod p (prime modulator)
If we further define X as (peer 1 private key) ^ (peer 2 private key) (which by observation could be written as (peer 2 private key) ^ (peer 1 private key)) then we can design a public exchange that does not allow an evesdropper to find the shared secret key.
The exchange is shown in Figure 3.
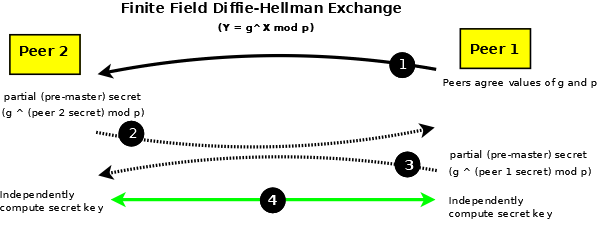
Figure 3 - Diffie Hellman Exchange
The two peers share p and g publicly (1). In some systems/protocols the initiator simply provides p and g, in others some form of peer negotiation takes place.
Peer 2 (2) then provides a partial result (sometimes called a pre-master secret) by computing g ^ (peer 2 private key) mod p and can send this publically to peer 1. In some protocols which use DH this partial result can be encrypted.
Peer 1 (3) in turn computes g ^ (peer 1 private key) mod p and can send this publically to peer 2 (some protocols can also encrypt this exchange). The order in which peer 1 and peer 2 compute and exchange the partial result is not significant.
In step (4) Peer 1 will take the partial result from peer 2 and raise it to its (peer 1 private key), effectively computing g ^ ((peer 2 private key) ^ (peer 1 private key)) = Y (the shared secret). Independently, Peer 2 will take the partial result from peer 1 and raise it to its (peer 2 private key), effectively computing g ^ ((peer 1 private key) ^ (peer 2 private key)) = the same value of Y (the shared secret). Figure 3 shows the common (or shared) sectret (4) being used to encrypt all subsequent traffic using some (previously agreed) symmetric algorithm.
This very short video does a terrific job of explaining the maths if you are into this stuff (unlike us).
Notes
In classic Finite Field Diffie-Hellman both p and g are typically small values, whereas the peer 1 and peer 2 secret keys are big, verging on huge.
If both peers use the same private key every time, then if either key is discovered the current exchange and all previous exchanges can be decrypted. It is not, in the jargon, forward secure. To avoid this one or both of the peers can generate a new private key in every Diffie-Hellman Exchange. This is known as a Ephemeral Diffie-Hellman exchange (typically, and confusingly, abbreviated to DHE).
Increasingly, algorithms other than Finite Field DH are being used, notably Elliptic Curves (EC). During the initial agreement(1) the curve type will be negotiated and then curve specific parameters publically exchanged. This is typically abbreviated to (EC)DH and if the exchange is ephemeral (EC)DHE.
The Diffie-Hellman exchange is always vulnerable to Man in the Middle attacks. Most protocols which use DH use some form of authentication, for example, TLS typically uses an x.509 certificate to authenticate at least one of the peers..

Message Digests (Hashes)
To provide data integrity, any message could be simply encrypted. In order to modify the data content of a message the attacker would have to be in possesion of the single key (in symmetric systems) or the private key (in asymmetric systems). However, encryption/decryption algorithms use complex mathematical functions, and are therefore heavy users of CPU resources. To encrypt all messages may incur unacceptably high overheads and this would be especially frustrating where data confidentiality is not a requirement. Fortunately, other techniques can be used to reduce this load. The most common is a lightweight procedure called a one-way hash, simply a hash, or more commonly a message digest (frequently shortened to just digest). The hash or digest algorithm creates a unique and relatively small fixed-size digest (irrespective of the original message length) that cannot be reversed. The resulting hash or digest is sometimes called a fingerprint since it uniquely describes or identifies the plain text. The messages being sent include both the plain text (unencrypted) and a digest of the message. The hash algorithm is applied to the received plain text and if the result matches the received message digest then the received data was not altered. The message digest is, in some senses, similar in concept to a checksum but has significantly different mathematical properties.
The most common forms of message digest are MD5 (Message Digest 5) and SHA-1 and increasingly SHA-224, SHA-256, SHA-384 and SHA-512 (the latter four being part of what is frequently called the Secure Hash Algorithm (SHA) SHA-2 family of digests). During August 2015 an SHA-3 algorithm was introduced by NIST. Figure 4 shows the message digest in action.
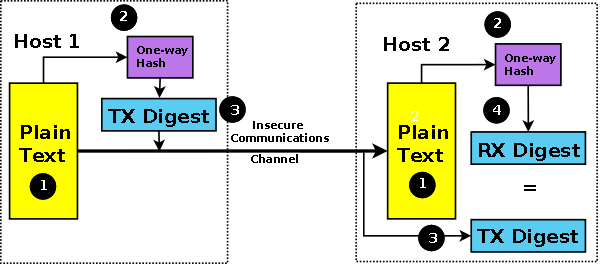
Figure 4 - Message Digest or One-Way Hash
Simply appending a message digest to a block of plain-text has the obvious weakness that by replacing both the plain text and its digest an attacker can subsitute or even introduce a rogue message.
Note: NIST SP800-107 Table 1 contains the relative strength of each hash or message digest.

Message Authentication Code (MAC)
The process of authentication and data integrity can use what is called a Message Authentication Code (MAC). The MAC combines the message digest with a shared (secret) key. The key part authenticates the sender, and the hash (or digest) part ensures data integrity. Two forms of MAC exist. A MAC based on a symmetric block cipher (such as TDEA or AES) is known as a CMAC. A MAC based on a hash (message digest) algorithm is known as a Hashed MAC (HMAC) and is, probably, the most widely used.
The most common forms of HMACs are HMAC-MD5 and HMAC-SHA-1 and increasingly HMAC-SHA-224, HMAC-SHA-256 and HMAC-SHA-384. Figure 5 shows how the MAC is used. The Secret Key used in HMAC may be generated by a variety of methods (defined in SP 800-107 rev1). At a simplified level this HMAC key can be viewed as simply salt whose purpose is to authenticate the source. Note: The MD5 hash algorithm, and by implication any algorithm that uses it, such as HMAC-MD5, has been moved to a "not recommended" status in most IETF documents, due to some theoretical weaknesses published in early 2005. These weaknesses do not invalidate the use of the algorithm but do indicate that is should be replaced with a more secure HMAC (HMAC-SHA-2 family) as soon as practical. Unfortunately HMAC-MD5 may be the only HMAC supported in many legacy systems.
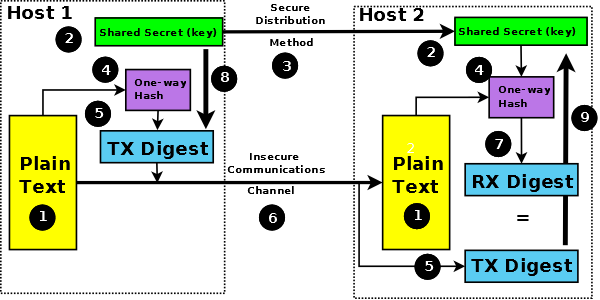
Figure 5 - Message Authentication Code (MAC)
The secret key (2) is distributed by some automagical or automated key management procedure (3) prior to communication. The plain text (1) is processed by the hash algorithm (4) to create a TX Digest (5) which is then enciphered (8) using the chosen algorithm and key (2). The message and enciphered TX digest is then send to the recipient using an insecure communications link (6). The recipient takes the plain text (1) runs it through the (same) hash algorithm (4) to create a RX digest (7). The received TX digest (5) is decipherd (9) using the chosen algorithm and key (2) and the resulting (plain text) TX digest compared with the RX digest (7). Equality = heaven, inequality = h.....orrible.
Figure 5 shows only the digest or hash being encrypted. This results in message integrity. If message confidentiality is also required then the entire message could be encrypted (covering both the plain text and the hash or digest). The TLS (SSL) protocol provides this latter capability in the Record Data phase.
<cryptographic terminology angst> The key shown in diagram 5 is labeled Secret Key: it is also a Private Key. It is labeled Secret Key since in order to remain a secret it would need to be kept actively private. Equally, and just as correctly, it could have been labeled Private Key (even though the term private key has overtones of asymmetric cryptography) since it must remain actively private in order to stay a secret. Life is soooo difficult sometimes. </cryptographic terminology angst>

Digital Signatures
In the asymmetric or public-key world, the process of authentication and data integrity uses what is called a digital signature. The message being sent is again hashed to create a message digest using, say, MD5, SHA-1, SHA-256 or SHA-384 to ensure data integrity. The resulting message digest is then encrypted using the private key of the sender (this is the reverse of public key confidentiality encryption - see note below). Both the plain-text message and the encrypted digest are sent to the receiving party. The receiver decrypts the message digest using the public key of the sender, applies the hash algorithm to the plain-text data, and if the results match, then both the authenticity of the sender and the integrity of the data are assured.
The most common digital signature algorithms are RSA-MD5, RSA-SHA-1, RSA-SHA-256, RSA-SHA-384, DSA (Digital Signature Algorithm: a US Government standard defined in FIPS-186 rev 4) and ECDSA (Elliptic Curve Digital Signature Algorithm - defined in FIPS-186 rev 4). Typical key sizes for RSA and DSA digital signature systems are 768 bits, 1024 bits, or increasingly 2048 bits (the current US NIST recommendation to cover the period from 2010 until 2030), or even higher values. Key sizes for ECDSA digital signatures are significantly smaller for the same level of security and are typically 112, 128, 192, 256 bits. Figure 6 shows how the digital signature is used. Note: The MD5 hash algorithm, and by implication any algorithm that uses it, such as RSA-MD5, has been moved to a "not recommended" status in most IETF documents, due to some theoretical weaknesses published in early 2005. These weaknesses do not invalidate the use of the algorithm and indeed legacy software continues to use it.
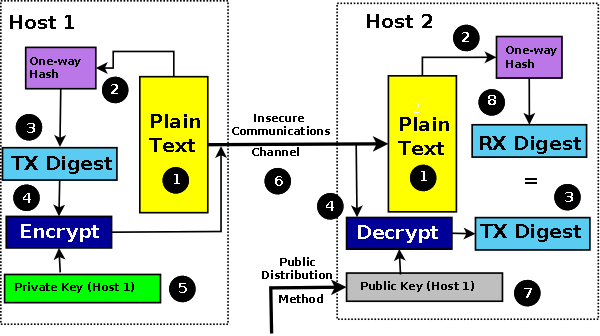
Figure 6 - Digital Signature
Note: In the above diagram while anyone can decrypt the message and recover the digest using the universally available public key, only the possessor of the private key can encrypt it - thus proving the authenticity of the source. The underlying digest provides the message integrity and, since it is encrypted by the senders private key, cannot be modified in transit. This use is in contrast to confidentiality in which the sender encrypts the data using the public key of the recipient, in which case only the private key of the recipient can decipher the message.

Problems, comments, suggestions, corrections (including broken links) or something to add? Please take the time from a busy life to 'mail us' (at top of screen), the webmaster (below) or info-support at zytrax. You will have a warm inner glow for the rest of the day.